# 몬테카를로 시뮬레이션

몬테카를로 시뮬레이션(Monte Carlo Simulation)이란 임의의 무작위수들(Random Numbers)을 이용한 반복적인 연산을 통해 특정 함수(들)의 결과 값을 확률적(Probabilistic)으로 계산해 내는 알고리즘입니다. 여기서 확률적 계산이란 결정적(Deterministic) 계산과 대비되는 개념으로서, 이는 필연적으로 알고리즘의 반복과 방대한 양의 계산을 수반하기 때문에 기계를 활용한 수치셈(Computational Calculation)과 함께 언급되는 것이 일반적입니다.

몬테카를로 시뮬레이션은 폴란드 출신의 수학자인 스타니스와프 울람(Stanislaw Ulam)이 개발하였으며 ‘예측이 어려운 결과에 대해서는 반복적 실험을 통해 예상되는 확률을 알아낼 수 있다’는 생각에 기초하여 도박으로 유명한 모나코의 도시 몬테카를로(Monte Carlo)의 이름을 따서 몬테카를로 시뮬레이션을 만들었다고 합니다.

# 예제

아래에서는 제가 마시모 디 피에로, 『파이썬으로 배우는 실전 알고리즘』, 프리렉(2015), p308-p329의 사례를 참조하여 조금 더 이해하기 쉬운 새로운 예제를 만들어 보았습니다.

1,000원짜리 상품을 판매하는 (주)폭망은 요즘 재고가 자꾸 쌓이는 것 같아 고민이다. (주)폭망의 사장님은 오랜 경험을 통해 하루 평균 방문 고객 수는 557명, 표준편차는 183명인 정규분포를 따른다는 것을 알고 있으며, 방문 고객은 재고가 있는 경우 5%의 확률로 구매를 하고, 재고가 없는 경우 (주문 예약을 통해) 2.5%의 확률로 구매를 한다는 것도 대략적으로 알고 있다. (주)폭망의 재고유지비는 하루 300원이다.

위 요소들을 모두 반영하는 단일의 최적화 모델을 수식화 하는 것은 확률의 형태로 표현된 불확실성으로 인해 쉽지 않습니다. 대신 각 방문자를 가정에 따라 모델링 하여 몬테카를로 시뮬레이션을 통해 최적의 재고수준을 구하는 것은 의외로 어렵지 않다는 점을 아래 코드를 통해 알 수 있습니다.

import random
import pandas as pd
import matplotlib.pyplot as plt

def sim(stock):
    gain = 0
    loss = 300*stock
    for p in range(int(random.gauss(557, 183))):
        if stock > 0:
            if random.random() < 0.05:
                stock -= 1
                gain += 1000
        else:
            if random.random() < 0.025:
                gain += 1000

    return gain-loss

def iter_sim(max_stock, how_many):
    final = []
    for _ in range(how_many):
        result = []
        for stock in range(1, max_stock):
            result.append(sim(stock))

        final.append(result)

    # 시각화
    plt.style.use('seaborn-whitegrid')
    output = pd.DataFrame(final)
    ax = output.T.plot(lw=0.1, color='black', legend=False)
    ax.set_xlabel("Stock")
    ax.set_ylabel("Gain / Loss")

    output.mean().plot(lw=5, color='red', legend=False)
    plt.show()


if __name__ == '__main__':
    iter_sim(150, 100)

# 결론

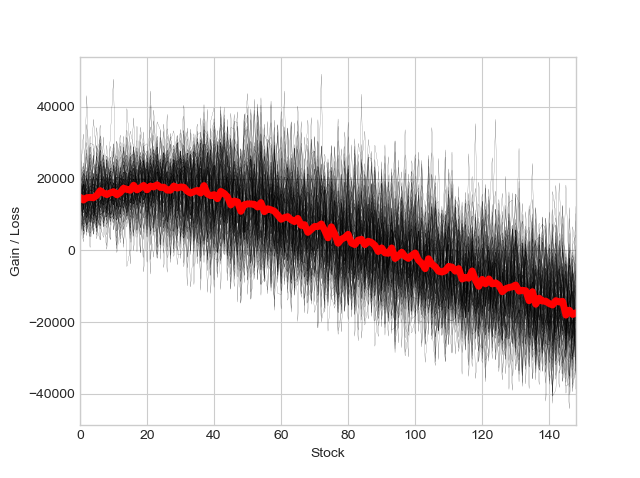
결과를 간단하게 시각화해보면 아래와 같으며, 매우 얇게 표현된 검은 선 하나 하나가 보유 재고 수준별로 가정된 분포를 따르는 방문자수에 대해 수행된 시뮬레이션이고, 이를 약 100회 반복한 결과를 보실 수 있습니다. 보다 효과적인 분석을 위해 해당 시뮬레이션들의 평균을 두꺼운 붉은색 선으로 표기한 결과, 사례의 경우에는 대략 20여개 수준의 여유 재고를 유지하는 것이 '(1) 확률적으로, (2) 재고유지비용과 손익을 고려하여'' 최적임을 보여주고 있습니다.

위 예제에서 느끼셨겠지만 구현 자체가 어렵지도 않고, 꽤 재미도 있으며 무엇보다도 마음만 먹으면 충분히 실무에 응용도 할 수 있습니다. 제 경우에는 다변수 재고 모형(BOM을 고려한 조립품의 재고 배합)에 대해 최적의 KPI를 찾기 위해 유사한 시뮬레이션을 구현한 적이 있습니다. 또 다른 재미있고 좋은 사례가 있으시다면 제게도 소개해주시면 감사하겠습니다.